Winograd 算法

在上一节的介绍中，介绍了 Im2Col 技术，它通过将三维张量重新排列成矩阵形式，然后利用基于内存访问局部性的优化库如 GEMM（通用矩阵乘法库）加速计算。随后，还探讨了空间组合优化，这一种利用局部性原理来提升效率的技术。

在本节将重点介绍 Winograd 优化算法，它是矩阵乘优化方法中 Coppersmith–Winograd 算法的一种应用，按照 Winograd 算法的原理将卷积的运算进行转换，从而减少卷积运算中乘法的计算总量。其主要是通过将卷积中的乘法使用加法来替换，并把一部分替换出来的加法放到卷积权重的提前处理阶段中，从而实现卷积计算的加速。Winograd 算法的优化局限于一些特定的常用卷积参数，这限制了其在更广泛场景下的应用。尽管存在这些局限性，Winograd 算法仍然是深度学习领域中的重要优化手段之一，对于提高卷积神经网络运行效率具有显著作用。

Winograd 算法原理

Winograd 算法最早是 1980 年由 Shmuel Winograd 提出的《Arithmetic complexity of computations》，当时并没有引起太大的轰动。在 CVPR 2016 会议上，Lavin 等人在《Fast algorithms for convolutional neural networks》中提出了利用 Winograd 加速卷积运算，于是 Winograd 加速卷积在算法圈里火了起来，并从此 Winograd 算法在包括 Mindspore Lite，MMN 等推理引擎中被广泛应用。

那 Winograd 为什么能加速卷积运算呢？简单来说就是用更多的加法计算来减少乘法计算，从而降低计算量，接下来就进一步了解如何使用 Winograd 加速卷积运算。

加速一维卷积计算

以一维卷积 \(F(2,3)\) 为例，假设输入信号为 \(d=[d_0,d_1,d_2,d_3]^T\)，卷积核为 \(g=[g_0,g_1,g_2]^T\)，则整个卷积过程可以转换为如下的矩阵乘形式：

\[\begin{split} \begin{align} F(2,3) = \begin{bmatrix} d_0 & d_1 & d_2\\ d_1 & d_2 & d_3 \end{bmatrix} \begin{bmatrix} g_0 \\ g_1 \\ g_2 \end{bmatrix} = \begin{bmatrix} r_0 \\ r_1 \end{bmatrix} \end{align} \end{split}\]

如果是使用一般的矩阵乘法进行计算，则如下式所示，会进行 6 次乘法操作与 4 次加法操作。

\[\begin{split} \begin{align} r_0 & = d_0 \times g_0 + d_1 \times g_1 + d_2 \times g_2\\ r_1 & = d_1 \times g_0 + d_2 \times g_1 + d_3 \times g_2 \end{align} \end{split}\]

具体的过程可以由下图了解到，在卷积的计算过程中，由于在卷积层的设计中，往往卷积的步幅（Stride）的大小会小于卷积核的大小，所以最后转换的矩阵乘中往往有规律的分布着大量重复元素，比如这个一维卷积例子中矩阵乘输入矩阵第一行的 \(d_1\)、\(d_2\) 和第二行中的 \(d_1\)、\(d_2\)，卷积转换成的矩阵乘法比一般矩阵乘法的问题域更小，这就让优化存在了可能。

在 Winograd 算法中则是通过增加加法操作来减少乘法操作从而实现计算加速，具体操作如下式所示：

\[\begin{split} \begin{align} F(2,3) = \begin{bmatrix} d_0 & d_1 & d_2\\ d_1 & d_2 & d_3 \end{bmatrix} \begin{bmatrix} g_0 \\ g_1 \\ g_2 \end{bmatrix} = \begin{bmatrix} m_1 + m_2 + m_3 \\ m_2 - m_3 - m_4 \end{bmatrix} \end{align} \end{split}\]

其中，\(m_1=(d_0-d_2)g_0\)，\(m_2=(d_1+d_2)\frac{g_0+g_1+g_2}{2}\)，\(m_3=(d_2-d_1)\frac{g_0-g_1+g_2}{2}\)，\(m_4=(d_1-d_3)g_2\)。

因为在推理阶段卷积核上的元素是固定的，所以上式 \(m_1\)，\(m_2\)，\(m_3\)，\(m_4\) 的式子中和 \(g\) 相关的式子可以提前计算好，在预测阶段只需要计算一次，因此计算次数可以忽略。而在计算 \(m_1\)，\(m_2\)，\(m_3\)，\(m_4\) 需要通过 4 次乘法操作与 4 次加法操作，然后基于计算好的 \(m_1\)，\(m_2\)，\(m_3\)，\(m_4\) 的值，需要通过使用 4 次加法操作得到结果，所以这里一共需要 4 次乘法操作和 8 次加法操作。由于乘法操作比加法操作消耗的时间多，因此 Winograd 的 4 次乘法和 8 次加法是要比一般的矩阵乘法的 6 次乘法和 4 次加法要快的。

而 Winograd 加速卷积计算的具体推导过程如下，由上面的式子可以得知：

\[\begin{split} \begin{align} m_1 + m_2 + m_3 &= d_0 \times g_0 + d_1 \times g_1 + d_2 \times g_2\\ m_2 - m_3 - m_4 &= d_1 \times g_0 + d_2 \times g_1 + d_3 \times g_2 \end{align} \end{split}\]

其中，因为 \(m_1\) 与 \(m_4\) 没有重复出现，所以令 \(m_1 = d_0 \times g_0\)，\(m_4 = -d_3 \times g_2\)，这样就可以约掉 \(m_1\) 和 \(m_4\)，所以左边的式子只剩下两个变量，两个等式两个变量即可求出 \(m_2\) 与 \(m_3\)，在这个时候的 \(m_1\)、\(m_2\)、\(m_3\)、\(m_4\) 是这样的：

\[\begin{split} \begin{align*} m_1 &= d_0 \times g_0\\ m_2 &= \frac{g_1d_1 + g_2d_2 + g_0d_1 + g_1d_2}{2} \\ m_3 &= \frac{g_1d_1 + g_2d_2 - g_0d_1 - g_1d_2}{2} \\ m_4 &= -d_3 \times g_2\\ \end{align*} \end{split}\]

\(m_2\) 中包含了 \(d_1\)、\(d_2\)、\(g_0\)、\(g_1\)、\(g_2\)，将这个式子转换为两个多项式乘积的形式，也即拆成 \(d\) 和 \(g\) 分开的形式，如下：

\[ \begin{align*} m_2 = \frac{(d_1 + d_2)(g_0 + g_1 + g_2)}{2} - \frac{d_2g_0}{2} - \frac{d_1g_2}{2} \end{align*} \]

同理，也对 \(m_3\) 进行转换得：

\[ \begin{align*} m_3 = \frac{(d_2 - d_1)(g_0 - g_1 + g_2)}{2} - \frac{d_2g_0}{2} + \frac{d_1g_2}{2} \end{align*} \]

由最初的(5)(6)式与上式可以得知，如果同时在 \(m_2\) 与 \(m_3\) 上同时加上一个值，对于式 (6) 来说整个式子是不变的，同时 \(m_4\) 的值没有改变，而对于式 (5) 来说需要减去两倍的这个值才能保持整个式子不变。因此，当这个值为 \(\frac{d_2 g_0}{2}\) 时可以简化表达式，通过这样的方式给上面的等式进行等价变换后得到的 \(m_1\)、\(m_2\)、\(m_3\)、\(m_4\) 如下：

\[\begin{split} \begin{align*} m_1 &= g_0(d_0 - d_2)\\ m_2 &= \frac{(d_1 + d_2)(g_0 + g_1 + g_2)}{2} - \frac{d_1g_2}{2} \\ m_3 &= \frac{(d_2 - d_1)(g_0 - g_1 + g_2)}{2} + \frac{d_1g_2}{2} \\ m_4 &= -d_3 \times g_2\\ \end{align*} \end{split}\]

同理，如果给 \(m_2\) 加上一个值，同时给 \(m_3\) 减去这个值，那么对于式 (5) 来说整个式子是不变的，并且 \(m_1\) 的值没有改变，对于式 (6) 来说需要给 m4 需要减去两倍的这个值才能保持整个式子不变。因此，当这个值为 \(\frac{d_1 g_2}{2}\) 时可以简化表达式，通过这样的方式给上面的等式进行等价变换后得到的 \(m_1\)、\(m_2\)、\(m_3\)、\(m_4\) 如下：

\[\begin{split} \begin{align*} m_1 &= g_0(d_0 - d_2)\\ m_2 &= \frac{(d_1 + d_2)(g_0 + g_1 + g_2)}{2} \\ m_3 &= \frac{(d_2 - d_1)(g_0 - g_1 + g_2)}{2} \\ m_4 &= g_2(d_1-d_3)\\ \end{align*} \end{split}\]

将上面的计算过程写成矩阵的形式如下：

\[ \begin{align} Y = A^T[(Gg)\odot (B^Td)] \end{align} \]

其中，

• \(\odot\) 表示 element-wise multiplication（Hadamard product），即对应位置相乘操作；

• \(g\) 表示卷积核；\(d\) 表示输入特征图（输入信号）；

• \(G\) 表示卷积核变换矩阵，尺寸为 \((u+k-1) \times k\)；

• \(B^T\) 表示输入变换矩阵，尺寸为 \((u+k-1)\times (u+k-1)\)；

• \(A^T\) 表示输出变换矩阵，尺寸为 \((u+k-1) \times u\)；

• \(u\) 表示输出尺寸，\(k\) 表示卷积核尺寸，\(u+k-1\) 表示输入尺寸。

式子中各个矩阵具体的值如下：

\[\begin{split} \begin{align*} & B^T=\begin{bmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 1 & 0 & -1 \end{bmatrix} \qquad G=\begin{bmatrix} 1 & 0 & 0 \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ 0 & 0 & 1 \\ \end{bmatrix} \qquad A^T = \begin{bmatrix} 1 & 1 & 1 & 0 \\ 0 & 1 & -1 & -1 \\ \end{bmatrix} \\ & g = \begin{bmatrix} & g_0 & g_1 & g_2 \end{bmatrix}^T \qquad \qquad d = \begin{bmatrix} d_0 & d_1 & d_2 & d_3 \end{bmatrix}^T \end{align*} \end{split}\]

加速二维卷积计算

将一维卷积 \(F(2,3)\) 的变换扩展到二维卷积 \(F(2 \times 2, 3 \times 3)\)，同样用矩阵形式表示为：

\[ \begin{align} Y = A^T[[GgG^T]\odot[B^TdB]]A \end{align} \]

其中，\(g\) 为 \(r \times r\) 的卷积核，\(d\) 为 \((m + r -1) \times (m + r -1)\) 的图像块.

对于二维卷积，可以先将卷积过程使用 img2col 进行展开，将卷积核的元素拉成了一列，将输入信号每个滑动窗口中的元素拉成了一行，变成如下的矩阵乘的形式：

\[\begin{split} \begin{align*} \begin{bmatrix} k_{0} & k_{1} & k_{2} & k_{4} & k_{5} & k_{6} & k_{8} & k_{9} & k_{10} \\ k_{1} & k_{2} & k_{3} & k_{5} & k_{6} & k_{7} & k_{9} & k_{10} & k_{11} \\ k_{4} & k_{5} & k_{6} & k_{8} & k_{9} & k_{10} & k_{12} & k_{13} & k_{14} \\ k_{5} & k_{6} & k_{7} & k_{9} & k_{10} & k_{11} & k_{13} & k_{14} & k_{15} \\ \end{bmatrix}\begin{bmatrix} w_0\\ w_1\\ w_2\\ w_3\\ w_4\\ w_5\\ w_6\\ w_7\\ w_8\\ \end{bmatrix}=\begin{bmatrix} r_0\\ r_1\\ r_2\\ r_3 \end{bmatrix} \end{align*} \end{split}\]

然后，将上述的矩阵乘的形式进行如下图的分块：

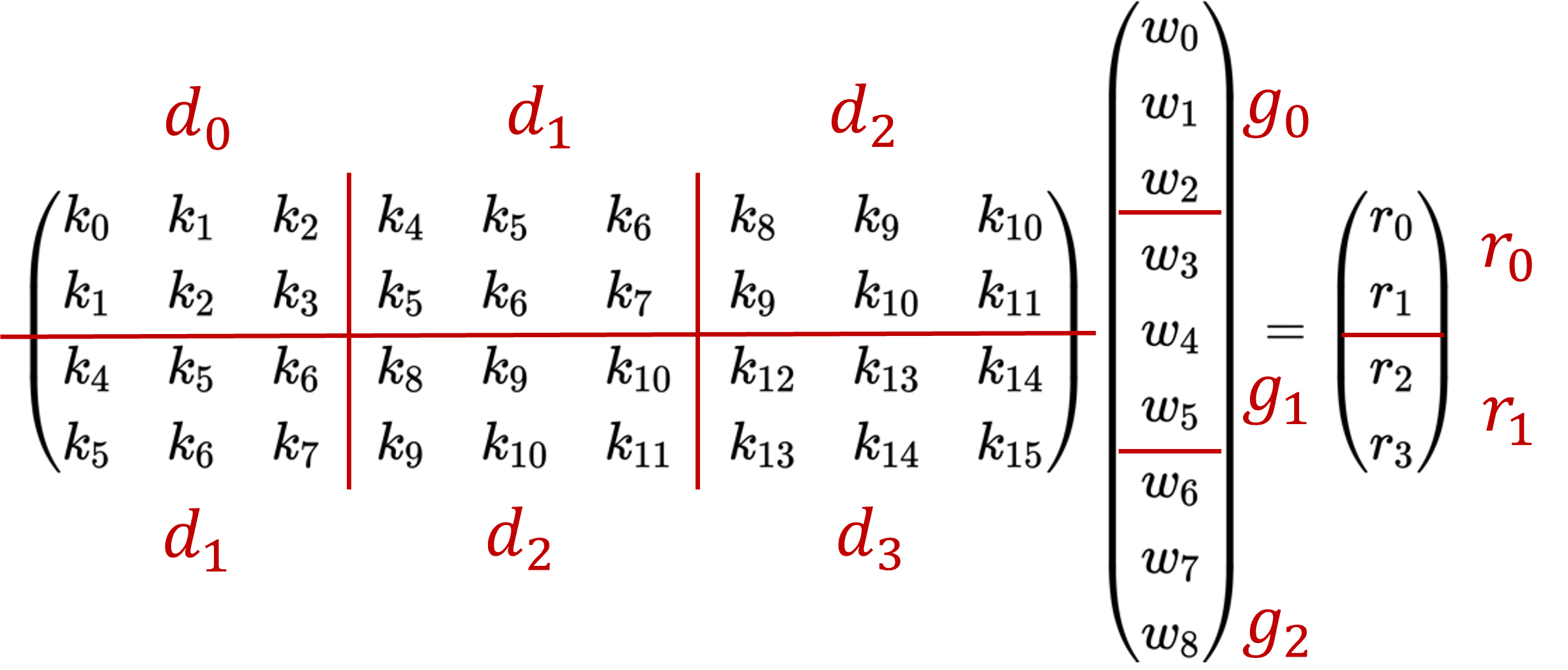
即可以表示成如下类似于前文中 Winograd 加速一维卷积计算形式：

\[\begin{split} \begin{align*} F(2 \times 2, 3 \times 3)=\begin{bmatrix} d_0 & d_1 & d_2\\ d_1 & d_2 & d_3 \end{bmatrix} \begin{bmatrix} g_0 \\ g_1 \\ g_2 \end{bmatrix} = \begin{bmatrix} r_0 \\ r_1 \end{bmatrix} \end{align*} \end{split}\]

当然，变成了这样的形式就可以使用前文的推导方法，推导到出式(8)中的 Winograd 加速二维卷积计算的矩阵形式。

Winograd 实现步骤

基于上文的介绍，Winograd 算法的实现可以细分为四个主要步骤：

1. 对输入卷积核的变换：\(𝑈=𝐺𝑔𝐺^𝑇\)，其中 \(G\) 表示为卷积核变换矩阵，\(g\) 表示卷积核

2. 对输入数据的变换：\(𝑉=𝐵^𝑇 d𝐵\)，其中 \(B\) 表示为输入数据的变换矩阵，\(d\) 表示输入的特征图

3. 对中间矩阵 M 的计算：\(M = \sum U \odot V\)

4. 卷积结果的计算：\(𝑌=𝐴^𝑇𝑀𝐴\)，其中 \(A\) 表示输出变换矩阵

Winograd 算法的工作流程可以用以下图示来说明：

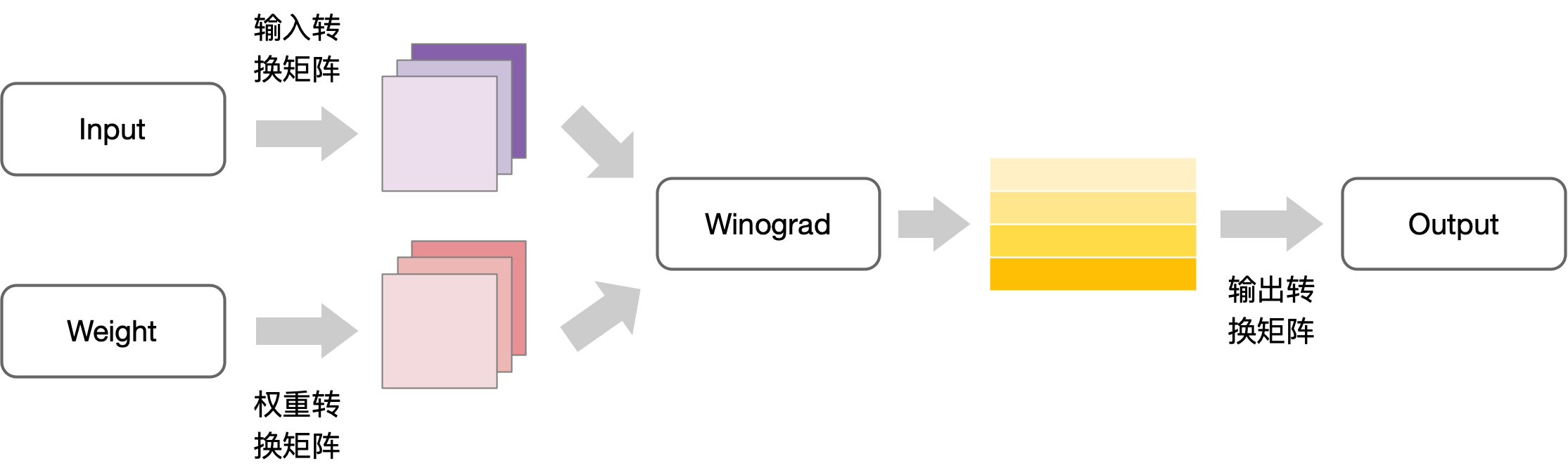
以上文中 Winograd 加速二维卷积 \(F(2 \times 2, 3 \times 3)\) 的计算为例子，可以具体了解 Winograd 的实现过程。

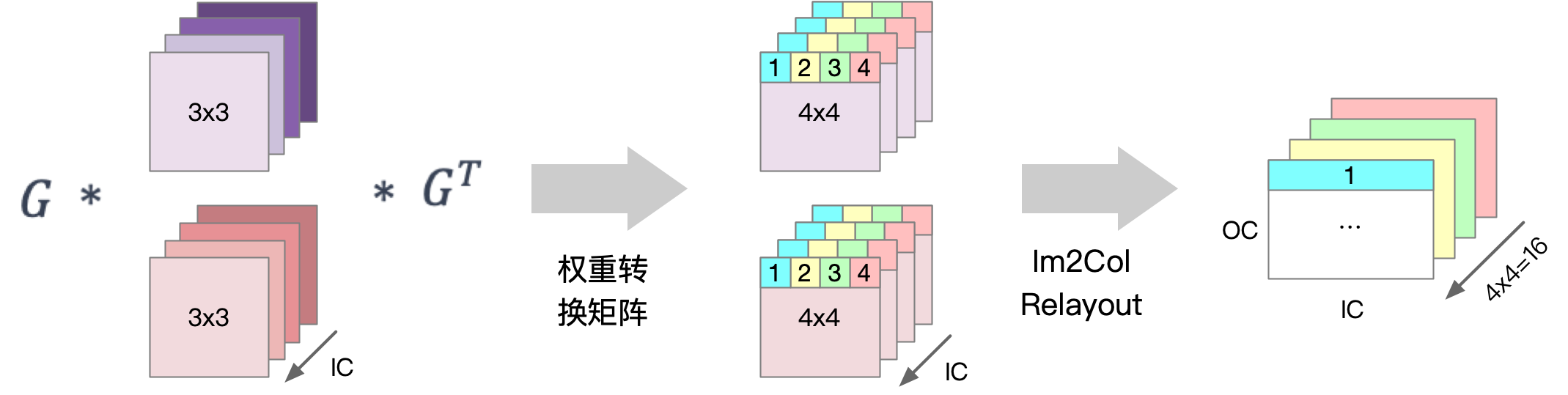
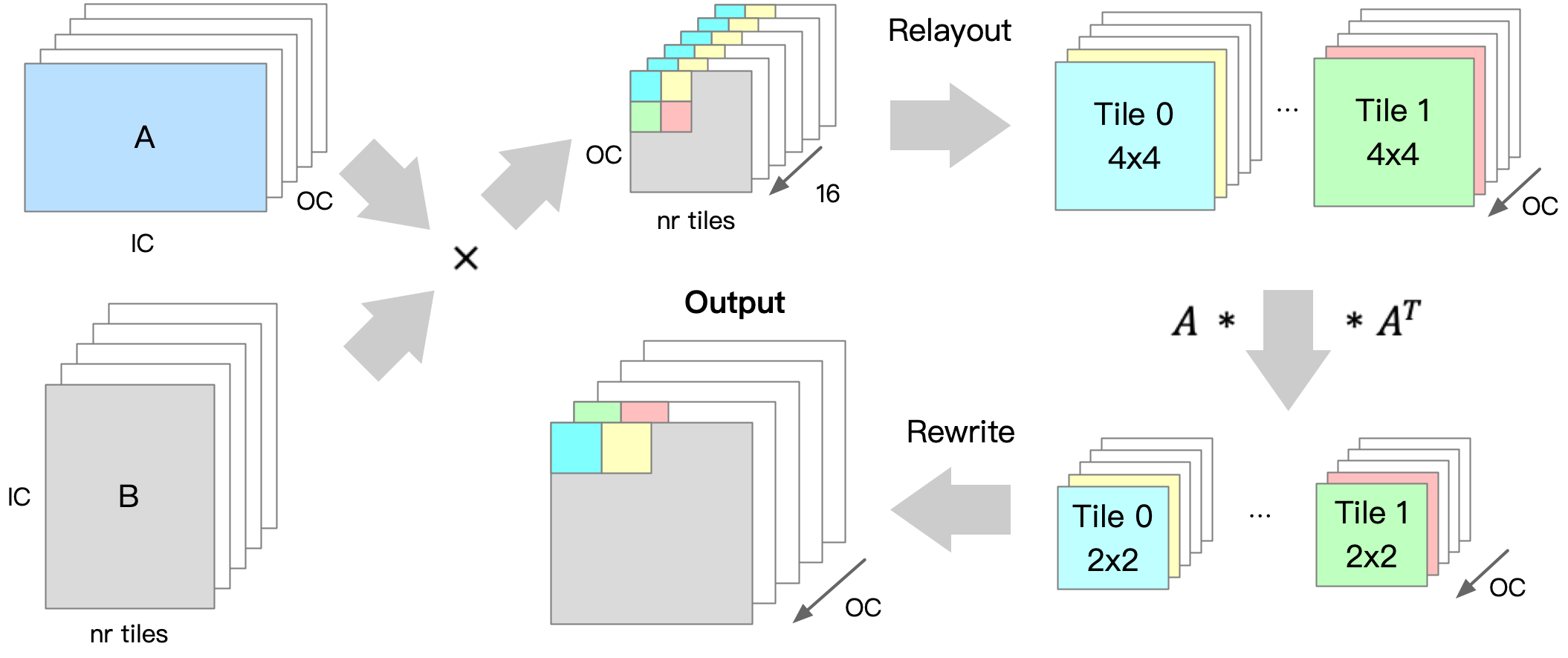
如下图所示，在输入卷积核的转换过程中，首先通过 Winograd 算法中的卷积核变换矩阵 \(G\) 和 \(G^T\) 分别将 \(3 \times 3\) 的卷积核权重转换为 \(4 \times 4\) 的矩阵。然后，将该矩阵中相同位置的点（如下图中蓝色为位置 1 的点）进行重新排布（Relayout），形成一个输入通道数 \(IC \times\) 输出通道数 \( OC\) 的矩阵，这一过程最终产生了 \(4 \times 4 = 16\) 个转换后的卷积核权重矩阵 \(U\)。

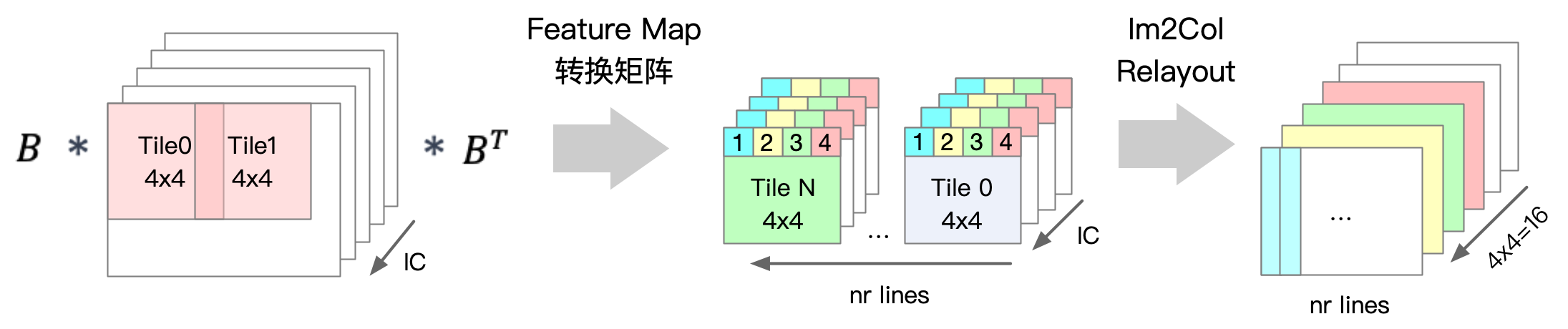
如下图所示，在输入数据的转换过程中，首先将输入数据切分成 \(4 \times 4\) 的小块（tile）。接着，通过 Winograd 算法中输入数据的变换矩阵 \(B\) 和 \(B^T\) 将每个小块转换为 \(4 \times 4\) 的矩阵形式。完成矩阵转换后，每个小块的数据按照与卷积核转换过程中类似的重新排布方法，转换成 16 个维度是小块数 \(nr\ tiles \times\) 输入通道数 \(IC\) 的输入数据矩阵 \(V\)。

如下图所示，将上述转换得到的卷积核权重矩阵 \(U\) 与输入数据矩阵 \(V\) 进行矩阵乘的操作，得到 16 个维度为小块数 \(nr\ tiles \times\) 输出通道数 \(OC\) 的中间矩阵 \(M\)。

随后，将相同位置的 16 个点重新排布成 \(nr\ tiles \times OC\) 个维度为 \(4 \times 4\) 的矩阵。然后再使用 Winograd 算法中的输出变换矩阵 \(A\) 和 \(A^T\) 将这些 \(4 \times 4\) 的矩阵转换为 \(2 \times 2\) 的输出矩阵，最后将这些矩阵写回输出矩阵中就可以得到 Winograd 卷积的最终结果 \(Y\)。

算法约束与缺点

从上述方法的介绍中可以得知，Winograd 算法通过减少乘法操作的次数，有效降低了计算资源的消耗，从而提高了计算速度。尽管 Winograd 算法在加速卷积运算方面有明显优势，但同时也存在一些局限性和不足之处。

首先，当应用 Winograd 算法处理单个小局部的二维卷积时，该算法不能直接应用于这样的计算当中，因为产生的辅助矩阵规模过大，可能会对实际效果产生负面影响。另外，不同规模的卷积需要不同规模的辅助矩阵，实时计算出这些辅助矩阵不现实，如果都存储起来会导致规模膨胀。

Winograd 算法虽然通过减少乘法次数来提高计算速度，但加法运算的数量却相应增加，同时还需要额外的转换计算和存储转换矩阵。随着卷积核和分块尺寸的增大，加法运算、转换计算和存储的开销也随之增加。此外，分块尺寸越大，转换矩阵也越大，计算精度的损失也会进一步加剧。因此，Winograd 算法仅适用于较小的卷积核和分块尺寸。在实际工程应用中，Winograd 算法通常只用于处理一些特定的 \(3 \times 3\) 卷积，而 \(1 \times 1\) 和 \(7 \times 7\) 、 \(5 \times 5\) 的卷积则不会采用 Winograd 这个 kernel。因此，在 runtime 中需要根据具体情况进行决策，选择合适的 kernel。

在实际应用中，通常会将所有可以固定的数据在网络运行前预先确定。在算法程序的设计中，希望尽可能提前计算出可以固定的数据，因此会有一个预编译阶段或离线模块转换阶段，以便提前计算出一些可预知的结果。在推理引擎中，主要处理的是一些常见或通用的算法问题，以及一些通用的网络模型结构。对于一些特定的网络模型结构，如果 \(G\) 是固定的，那么可以将特定网络的 \(G\) 提前计算出来，这样在下次运行时，就不需要重新计算。例如，在设计基于 Winograd 算法的特定网络结构时，如果 \(G\) 和 \(g\) 是固定的，那么 \(U=GgG^T\) 可以在网络运行前预先确定。

另一个想法是将 Winograd 算法与空间组织算法结合起来，充分利用局部性和算法分析的优化，将卷积计算通过空间组合优化算法中的拆分方法，将输入拆分成若干个小规模卷积。例如，可以拆分成每个小卷积输出 \(4 \times 4\) 个数据的卷积。

小结与思考

• Winograd 算法优化原理：通过减少乘法操作的数量，增加加法操作，利用卷积核和输入数据的变换矩阵，将卷积运算转换为更少乘法次数的等价形式，从而加速卷积计算。

• Winograd 算法实现步骤包括输入卷积核的变换、输入数据的变换、中间矩阵的计算，以及最终卷积结果的计算，涉及特定的矩阵乘法和元素乘积（Hadamard product）。

• Winograd 算法适用于特定的卷积核和分块尺寸，对于大规模卷积核或大尺寸分块，转换矩阵的规模和计算精度损失可能会降低算法效率。

• 在实际应用中，Winograd 算法可以与空间组织算法结合，通过分块处理和卷积核的预编译，优化计算过程，尤其适用于小型卷积核如 \(3×3\)。

本节视频