公共表达式消除原理

公共表达式消除原理#

公共子表达式消除（Common Subexpression Elimination，CSE）也成为冗余表达式消除，是普遍应用于各种编译器的经典优化技术。旨在消除程序中重复计算的公共表达式，从而减少计算量和提高执行效率。

传统编译器的公共子表达式消除#

概述#

在程序中，有时会出现多个地方使用相同的表达式进行计算，并且这些表达式的计算结果相同。重复计算这些表达式，会增加不必要的计算开销。公共表达式消除的目标就是识别出这些重复的计算，并将其提取出来，只计算一次，然后将结果保存起来供后续使用。

以下是一个简单的公共子表达式：

temp = b * c
a = b * c + g
d = b * c + e

在计算 a 和 d 的时候都使用到了 b * c 这个表达式，而该程序在计算 a 和 d 之前已经计算过 b * c 并将其计算结果保存在 temp 中，并且从 b * c 计算并赋值到 temp 后到计算 a 和 d 之间，b 或 c 的值并没有发生改变，则可以将计算 a 和 d 中的 b * c 替换成 temp，能够将以上代码转化成以下代码:

temp = b * c
a = temp + g 
d = temp + e

对于 b * c，程序只需要计算一次，并将结果保存在 temp 中，当计算 a 和 d 使用到时直接载入 temp 中保存的值即可，避免了 b * c 的重复计算，提高程序的执行效率。

编译器开发者将公共子表达式消除分成两类。如果这种优化仅限于程序的基本块内，便称为局部公共子表达式消除；如果这种优化范围涵盖了多个基本块，那就称为全局公共子表达式消除。

下面分别两种常见的公共子表达式消除方法，分别是局部值编号(LVN)和缓式代码移动(LCM)。局部值编号是一种常见的局部公共子表达式消除，它通过局部散列表，在找到并消除公共子表达式。缓式代码移动是一种常见的全局公共子表达式消除，它通过可用表达式，可预测表达式，延迟分析这三种数据流问题，将冗余表达式上提到合适的位置，从而消除公共子表达式的目的。

局部值编号#

局部值编号(Local Value Numbering, LVN)是一种局部公共子表达式优化算法，其主要目的就是为了识别并消除基本块中冗余的表达式。

LVN 会为每个基本块都维护一个散列表，用于存储该基本块中的变量，常量以及表达式的散列值。假设表达式形如 \( x\ op\ y\)，散列值用 \(VN()\) 表示，LVN 计算过程如下：

  1. 按顺序遍历所有的表达式。

  2. 分析表达式 \( x\ op\ y\) 的两个子表达式 x 和 y。查询散列表，若能查询到，则返回其所对应的散列值。若没查询到则创建一个新的表项以及散列值，插入到散列表中，并将新的散列值返回。

  3. 获得 \(VN(x)\) 和 \(VN(y)\) 后，计算 \(VN(\{VN(x)\ op\ VN(y)\})\),若能在散列表中找到该表达式对应的散列值，则说明该表达式在前面定义过了,可以将其替换成此前该表达式的计算值。如果没找到，则在生成一个新的表项以及对应的散列值，插入到散列表中。

缓式代码移动#

缓式代码移动(Lazy Code Motion, LCM)使用一种数据流分析技术，通过可用表达式，可预测表达式以及延迟分析这三种数据流问题的方程，实现全局的公共子表达式消除。

在缓式代码移动中，对于某个待优化的表达式 e，通常会生成一个新的表达式赋值，将 e 赋值到一个临时变量中，形如 \(h = x\ op\ y\), 其中 h 为临时变量，\(x\ op\ y\) 是待优化的表达式 e。

LCM 的算法实现主要分成两步：

  1. 将公共子表达式尽可能的往上提，即找到该表达式第一次被求值的位置，该过程称为最早放置。

  2. 公共子表达式在找到第一次被求值的位置后，如果直接插入可能会引起新的冗余，此时又需要将插入位置尽可能的下沉，并且保证下沉前后插入引起的结果相同。该过程称为延迟放置

可用表达式#

对于某个使用表达式e: x op y的操作d，如果在 d 上,e 是可用表达式当且仅当从程序入口到达操作 d 的所有路径都计算过 e，且从求值处到操作 d 之间，e 的任何一个子表达式的值都没有发生改变。

当一个表达式对于某个基本块是可用表达式，其含义为从入口基本块 \(b_0\) 到基本块 \(b_n\) 的入口处的所有路径都计算过 e，且从求值处到 \(b_n\) 的入口处，表达式 e 没有被杀死，即其任何一个子表达式都没有被重新计算过。

在控制流图中，编译器为每个基本块都维护一个可用表达式集合，记为 Availn(n)。定义 Availn(n)集合的公式如下：

\[ AvailIn(n) = \bigcap_{m\in{preds(n)}}(DEExpr(m) \cup (AvailIn(m) \cap \overline{ExprKill(m)})) \]

公式的初始条件为：\(b_0\) 为程序的入口节点，\(AvailIn(n_0) = \empty , AvailIn(n_i) = \{all\ expression\},\forall{n_i} \ne n_0 \)

其中：

  • preds(n) 表示基本块 \(b_n\) 所对应的前继节点集。

  • DEExpr(m) 表示基本块 \(b_m\) 中向下展示的表达式，即若表达式 \(e\in DEExpr\),则从表达式 e 的计算处到 \(b_m\) 基本块出口都未被重新赋值过。

  • \(\overline{ExprKill(m)}\) 表示在基本块 \(b_m\) 中未被杀死的表达式，即当一个表达式 \(e\in ExprKill(m)\),则表明该表达式存在一个或则多个子表达式在 \(b_m\) 中被重新计算了。

根据 \(AvailIn(n)\) 的计算公式可知，若表达式 \(e\in AvailIn(n)\) 当且仅当 e 是 \(b_n\) 前继节点中向下展示的表达式或 e 在 \(b_n\) 前继节点的入口和出口处都是可用表达式。

可预测表达式#

可预测表达式通常是针对基本块来说的，编译器会为每个基本块都维护一个可预测表达式集合，记为 \(AntOut(n)\)。其含义为若表达式 \(e\in AntOut(n)\)，则表示在 \(b_n\) 中出口处 e 的值可用于预测从 \(b_n\) 到出口节点的所有路径上所有表达式 e 的使用，即路径上所有使用的表达式 e 都是冗余的表达式。其计算公式如下:

\[ AntOut(n) = \bigcap_{m\in{succ(n)}}(UEExpr(m) \cup (AntOut(m) \cap \overline{ExprKill(m)})) \]

公式的初始条件为：\(b_f\) 为程序的出口节点，\(AvailIn(n_f) = \empty , AvailIn(n_i) = \{all\ expression\},\forall{n_i} \ne n_0 \)

其中：

  • succ(n) 表示基本块 \(b_n\) 的后继节点块。

  • UEExpr(m) 表示向上展示的表达式，即在基本块 \(b_m\) 中被杀死前所使用的表达式，即若表达式 \(e\in UEExpr(m)\),如果在 \(b_m\) 将对 e 的一个或多个子表达式进行修改，则这些修改操作位于使用 e 之后。

  • \(\overline{ExprKill(m)}\) 表示在基本块 \(b_m\) 中未被杀死的表达式，即当一个表达式 \(e\in ExprKill(m)\),则表明该表达式存在一个或则多个子表达式在 \(b_m\) 中被重新计算了。

根据 \(AntOut(n)\) 的计算公式可知，若表达式 \(e\in AntOut(n)\) 当且仅当 e 是 \(b_n\) 前继节点中向上展示的表达式或 e 在 \(b_m\) 后继继节点的入口和出口处都是可预测表达式。

最早放置#

由于进行最早放置需要使用基本块出入口的可用表达式和可预测表达式，而之前的两种数据流问题分析不够完全，下面分别给出补全的定义。

对于可用表达式，当已知基本块 \(b_n\) 的入口可用表达式为 \(AvailIn(n)\),则其出口可用表达式包含 \(b_n\) 中向下展示的表达式集合以及在入口处为可用的表达式，并且在 \(b_n\) 中没有被杀死的表达式集合。其定义为：

\[ AvailOut(n) = DEExpr(n) \cup (AvailIn(n) \cap \overline{ExprKill(n)}) \]

对于可预测表达式，当已知基本块 \(b_n\) 的出口可预测表达式为 \(AntOut(n)\),则其入口可预测表达式包含 \(b_n\) 中向上展示的表达式集合以及在出口处是可预测表达式，并且在 \(b_n\) 中没有被杀死的表达式集合。其定义为：

\[ AntIn(n) = UEExpr(n) \cup (AntOut(n) \cap \overline{ExprKill(n)}) \]

为了简化最早放置的过程分析，假设每条边含有一个存储集，记为 Earliest(i,j),其中 i 和 j 分别表示源节点和目的节点的编号，用于存储待优化的表达式。其含义为若表达式 \(e\in Earliest(i,j)\),则该表达式无法无法通过基本块 \(b_i\) 前往更早的边，即 \(b_i\) 为该表达式的最早赋值边界。其定义为：

\[ Earliest(i,j) = AntIn(j)\ \cap\ \overline{AvailOut(i)}\ \cap\ (ExprKill(i)\ \cup \overline{AntOut(i)}) \]

其中：

  • 若表达式 \(e\in AntIn(j)\)，根据入口可预测表达式的定义，从 \(b_j\) 的入口处到出口基本块，表达式 e 的任何一个子表达式都没有被重新定值，即可以安全的将表达式 e 移动到 \(Earliest(i,j)\) 中，这里的安全性表示将表达式 e 上移后，不会使其他不包含该表达式的路径引入该表达式，即不会产生新的冗余表达式。

  • 若表达式 \(e\in \overline{AvailOut(i)}\)，根据出口可用表达式的定义，这意味着从入口基本块到 \(b_i\) 的路径上，e 的一个或多个子表达式被重新定值。

  • 根据第二个条件，为了使得表达式 e 不能通过 \(b_i\) 前往更早的边，则 e 的子表达式重新定值需要发生在 \(b_i\) 中，所以此时表达式 \(e\in ExprKill(i)\)。如果表达式 \(e\in \overline{AntOut(i)}\),根据出口可预测表达式的定义，这意味着此时存在一个或者多个 \(b_i\) 的后继节点，表达式 e 在这些基本块的入口处不是可预测的，则说明表达式 e 的一个或多个子表达式在这些路径中被重新定值，此时表达式 e 甚至无法被移动到 \(b_i\) 中，就更不可能移动到更早的边上。这两个条件除非同时不满足，否则表达式不能移动到更早的边。

延迟放置#

在完成最早放置后，编译器会进行延迟分析。延迟分析是控制流图上的一个前向数据流问题，其主要目的是为了判断边上的某个待优化表达式能否通过其目的节点，进入到下一条边中。

编译器为每个基本块维护一个集合 \(LaterIn(n)\),其含义为若表达式 \(e\in LaterIn(n)\),则表达式 e 在 \(b_n\) 的入口处是可延迟的。为每条边维护一个集合 \(Later(i,j)\),其含义为若表达式 \(e\in Later(i,j)\),则表示表达式 e 可以进入到 \(b_j\) 中，直观上看 \(Later(i,j)\) 就是个可能下沉表达式集合。其定义如下：

\[\begin{split} LaterIn(j) = \bigcap_{i\in preds(j)}\ Later(i,j), j\ne n_0 \\ Later(i,j) = Earliest(i,j)\ \cup\ (LaterIn(i)\ \cap\ \overline{UEExpr(i)}),\ i\in preds(j) \end{split}\]

从公式上看，可能下沉表达式集合分为两部分。若表达式 \(e\in Earliest(i,j)\),则表达式 e 一定是可能下沉的表达式，而另一部分的表达式来自于 从 \(b_i\) 下沉下来的表达式，这些表达式满足在 \(b_i\) 的入口处是可下沉的，并且这些表达式在 \(b_i\) 不是向上展示的表达式，因为如果表达式 \(e\in UEExpr(i)\),则表明表达式在 \(b_i\) 中被求值，如果下沉，那么下沉的这个表达式则成为冗余表达式。

重写代码#

最后一步使用 \(LaterIn(n)\) 和 \(Later(i,j)\) 生成额外的集合指导编译器重写代码，额外集合包括 \(Insert(i,j)\) 和 \(Delete(i)\) 集合。

\(Insert(i,j)\) 表示可插入的集合。其定义如下：

\[ Insert(i,j) = Later(i,j)\ -\ (LaterIn(j)\ \cap \overline{UEExpr(j)}) \]

从公式上看，\(Later(i,j)\) 为可能下沉的集合，\(LaterIn(j)\ \cap \overline{UEExpr(j)}\) 表示可以从 \(b_j\) 下沉到底部的集合。所以去掉可能下沉集合中的所有能下沉的表达式，留下的就是不能下沉的表达式，即需要插入的表达式。

插入规则为：

  • 如果 \(b_i\) 只有一个后继节点 \(b_j\)，则将 \(Insert(i,j)\) 中的表达式插入到 \(b_i\) 的出口处。

  • 如果 \(b_j\) 只有一个前趋节点 \(b_i\)，则将 \(Insert(i,j)\) 中的表达式插入到 \(b_j\) 的入口处。

  • 若前两个条件都不满足，则在边 \({b_i\rightarrow b_j}\) 上新建一个基本块，将 \(Insert(i,j)\) 中的表达式插入到该基本块中。

需要注意的是，由于插入的是新的赋值语句，所以插入后，有一些表达式冗余了。比如对于一个基本块的向上展示的表达式。因此编译器对每个基本块都需要维护一个删除集合，记为 \(Delete(i)\)。其定义如下：

\[ Delete(j) = UEExpr(j)\ \cap \ \bigcup_{i\in preds(j)} Insert(i,j) \]

AI 编译器的公共表达式消除#

公共表达式是传统编译器常用的前端优化的一种，经过迁移也可以应用到深度学习编译器中。

AI 编译器中公共子表达式消除采取相同的思路，区别在于 AI 编译器中子表达式是基于计算图或图层 IR。通过在计算图中搜索相同结构的子图，简化计算图的结构，从而减少计算开销。

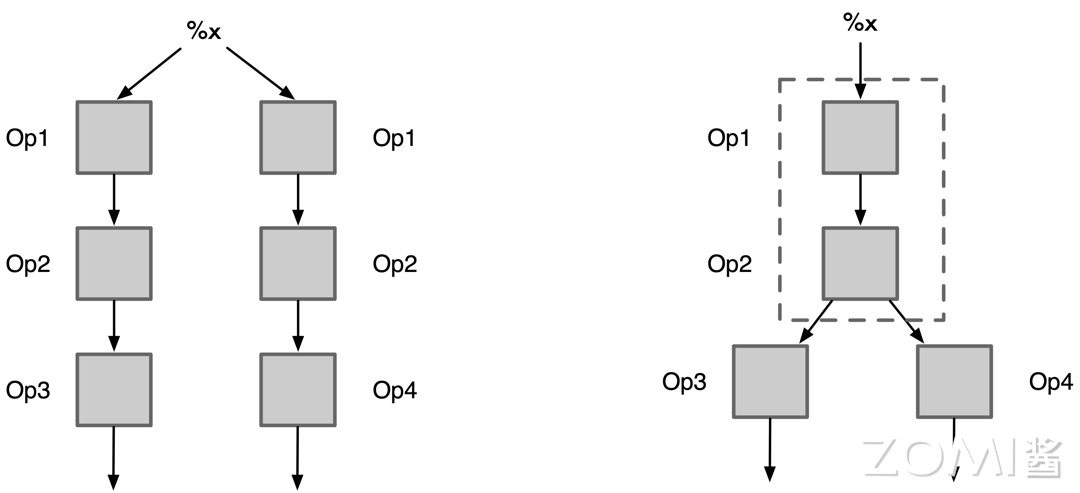
second

图中 Op3 和 Op4 都经过了相同的图结构\(\{\{Op1,Op2\},Op1\rightarrow Op2\}\), AI 编译器会将相同子图的所有不同输出都连接到同一个子图上，然后会在后续的死代码消除中删除其他相同的子图，从而达到简化计算图的目的。减少计算开销。

公共子表达式实现案例#

传统编译器实现案例#

支配性#

支配性的含义是对于入口基本块 \(b_0\) 以及任意基本块 \(b_i\) 和 \(b_j\)，其中 \(i\ne j\)。如果从 \(b_0\) 到 \(b_i\) 的所有路径都经过 \(b_j\) ，则称 \(b_j\) 是 \(b_i\) 的支配节点。

支配性是一个正向数据流问题。编译器会为每个基本块维护一个支配节点集合，记为 \(Dom(n)\)。计算公式如下：

\[ Dom(n) = {n}\ \cup \ (\bigcap_{m\in preds(n)}Dom(m)) \]

初始条件为：\(Dom(n_0) = n_0,\ Dom(n_i) = N\), 其中 N 是控制流图中所有节点的集合，\(i\ne 0\)。公式中的 \(preds(n)\) 表示 \(b_n\) 的前继节点集合。

静态单一赋值(SSA)#

SSA（Static Single Assignment）是一种中间表示（IR）形式，用于在编译器优化和静态分析中表示程序的数据流。SSA 形式中的每个变量在程序中只能被赋值一次，这样可以简化数据流分析和优化的过程。其含有以下特点：

  • 单一赋值：在 SSA 形式中，每个变量只能在程序中被赋值一次。这意味着每个赋值语句都会引入一个新的变量版本，用于存储该赋值的结果。

  • φ函数（Phi 函数）：在 SSA 形式中，当一个变量具有多个可能的来源时，使用φ函数来选择正确的值。φ函数接受来自不同基本块的变量版本，并在控制流中根据前驱基本块的条件选择正确的版本。

  • 显式使用：在 SSA 形式中，每个变量的使用都明确指定了其来源，即变量的定义。这使得数据流分析和依赖关系的跟踪更加直观和准确。

实现案例#

不同编译器在实现公共子表达式优化的细节上不尽相同，下面以 Golang 为例，介绍一种实现方式。Golang 是对 SSA IR 进行公共子表达式优化的。其算法步骤为：

  1. 粗粒度划分等价集。遍历所有的 Block，将值存储在一个数组 a 中，然后根据诸如操作类型，操作的数据类型，操作数类型等粗粒度判断标准进行排序，对于粗粒度标准相同的值按照值的 ID（值的标号）进行排序。排序完成后对数组 a 进行切分，将粗粒度标准相同的值切分到同一个数组中，然后存入粗粒度划分等价集中。

  2. 细粒度划分等价集。在进行后续处理之前，需要给粗粒度划分等价集中的每个集合中的值分配一个等价 ID。如果集合的个数大于 1，该集合为等价集，为该等价集里的每个值分配一个相同的正数等价 ID；如果个数等于 1，说明该集合为非等价集，为值分配一个负数等价 ID，其大小为该值的 ID。遍历粗粒度划分等价集中所有的等价集，按照细粒度标准进行划分。以 Add 为例：

    v1 = Const64 <int> [1]
v2 = Const64 <int> [2]
v3 = Const64 <int> [3]
v4 = Add64 <int> v1 v2
v5 = Add64 <int> v2 v3
v6 = Add64 <int> v2 v1

    在粗粒度等价集中存在一个等价集：

    {v4, v5, v6}

    将该等价集按照细粒度标准排序，即按照操作数的等价 ID 排序,由于加法满足交换律，在进行排序前，还需要将两个操作数按照等价 ID 进行从小到大的排序。可得：

    {v6, v4, v5}

    不难发现，v4 和 v5 的两个操作数是一模一样的，而又与 v6 不同，所以对该等价集进行切分，获得非等价集{v6}和等价集{v4，v5}。此时粗粒度等价集如下：

    {{v4, v5}, {v1}, {v2}, {v3}, {v6}}

    划分完成后，对粗粒度等价集重新分配等价 ID，然后继续上面的步骤，直到前后两次粗粒度等价集没有发生变化，此时得到细粒度等价集。

  3. 替换重复表达式。在细粒度等价集中的每一个等价集都可以看成是一组重复的表达式，但是这些表达式不能随意消除，需要判断 Value 所在的块是否支配需要替换的 Value 所在的块，如果支配则可以进行替换消除。

AI 编译器实现案例#

以 tensorflow 为例，给出 AI 编译器实现公共表达式消除的一种实现：

  1. 获得逆后续节点集。tensorflow 使用反向深度优先搜索遍历计算图，获得逆后续节点集。这样处理的目的是为了确保在处理某个节点时，其所有的输入节点已经处理完毕。

  2. 遍历逆后续节点集，由于公共子表达式优化只与操作节点有关，所以在遍历的时候忽略非操作节点。tensorflow 使用混合哈希的计算模式为每个操作节点计算其对应的哈希值。参与混合哈希计算的节点属性包括输出节点的个数，每个输出节点的类型，输入节点的信息等等。这样处理的目的是为了确保一个表达式对应一个 hash 值，达到检索公共表达式的目的。

  3. 维护公共子表达式候选集，将节点和哈希值一一对应，当处理一个新的操作节点时，判断该节点的哈希值是否在公共子表达式候选集中，如果不存在，则将该操作节点及其哈希值添加到公共子表达式候选集中。如果存在，则用公共子表达式候选集中的节点连接到该操作节点的所有输出节点，但对于该操作节点并不会做任何处理，这会在后续的死代码删除中被删除掉。

本节小结#

公共子表达式消除就是去掉程序中相同的结构，减少重复计算。传统编译器通过找到重复表达式，存储表达式的计算结果，并用该计算结果替换重复表达式的引用。AI 编译器通过找到相同的子图，将相同子图的所有输出都连接到同一个子图，从而达到公共子表达式消除的目的。

通过公共子表达式消除，可以减少重复计算和冗余代码，从而提高程序的性能。然而，需要注意的是，CSE 可能会增加代码的复杂性和内存消耗，因此在实际应用中需要权衡考虑。

本节视频#

Contents